Цель определить и компенсировать отклонение робота от заданного курса (направления)
Есть робот, схема робота представлена на рисунках
Все листинги можно скачать здесь!!! В статье приведены только небольшие участки кода

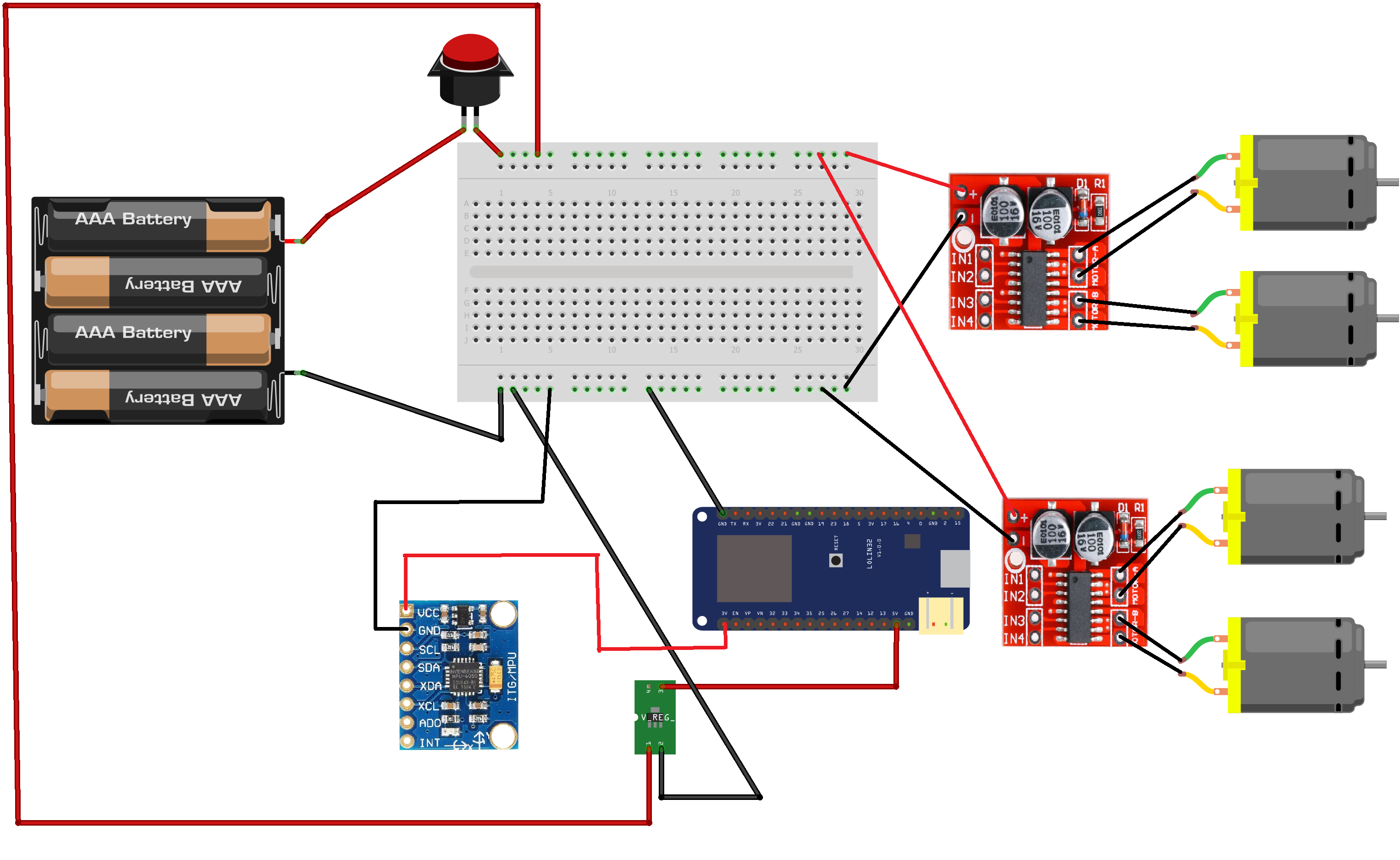
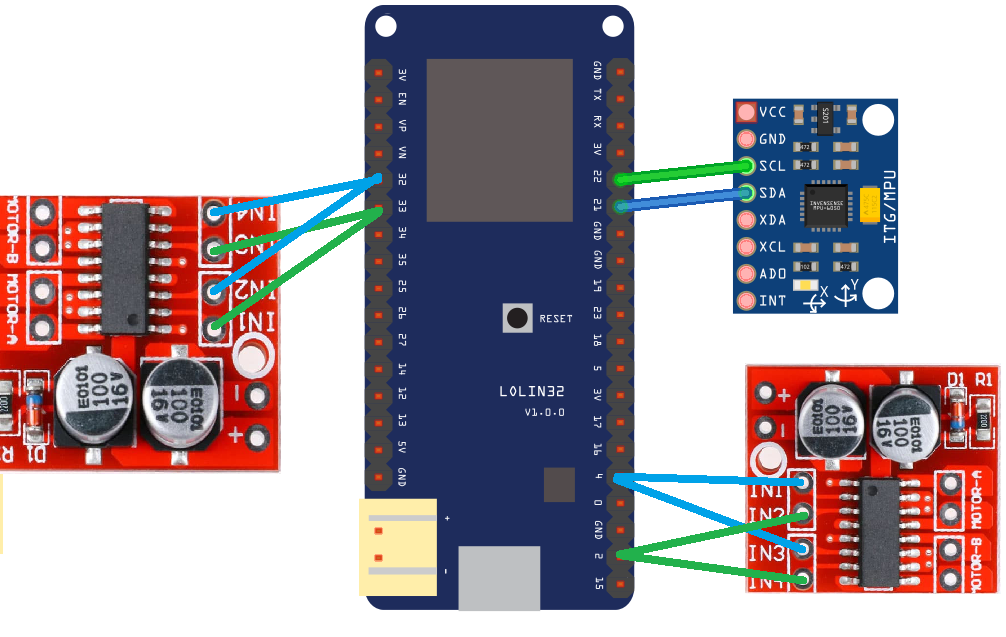
Задача определить и компенсировать отклонение робота от заданного курса (направления)
Разобьем задачу на две простые
- Определить отклонение робота от заданного направления
- Компенсировать отклонение робота от заданного направления
Задача 1. Определить отклонение робота от заданного направления
Если угловую скорость умножить на время действия этой скорость, то получим изменение текущего угла поворота по заданной оси:
- отклонение от курса после прошлого измерения,
, это изменение, которое претерпел угол поворота за время от предыдущего измерения до настоящего момента, назовем это время
. Тогда формулу можно записать:
Где
Пока робот двигается по абсолютно ровной поверхности, данная формула будет работать как надо, но если движение подразумевает, что робот изменяет не только угол поворота, но и отклоняется по другим осям, то подобные расчеты применять нельзя.
Обосновать это довольно просто, повороты в трехмерном пространстве вокруг любых двух осей из трех приводят к изменению угла порота по третей оси…
Пусть Ось Z направлена верх (рыскание), угол поворота по данной оси и должен быть измерен, ось X – пусть будет отвечать за наклон робота вперед – назад (тангаж), ось Y отвечает за наклон робота вправо-влево. Теперь поверните робота на 90 градусов по оси X, так, чтобы его нос смотрел вверх, затем поверните робота по оси Y на 90 градусов, а затем поставьте робота на поверхность еще одним (обратным) поворотом на 90 градусов по оси X. Теперь робот повернул по оси Z на 90 градусов, но все это время мы не имели поворотов по Z, и угловая скорость по Z была нулевой.
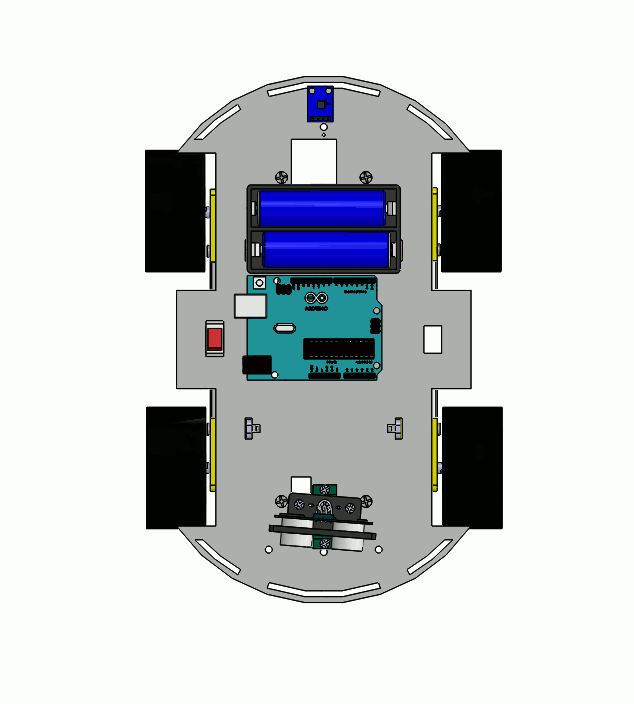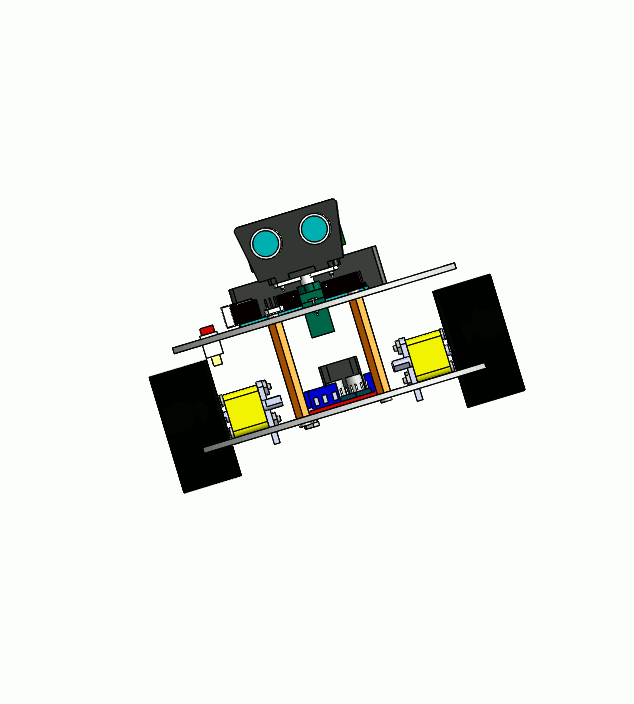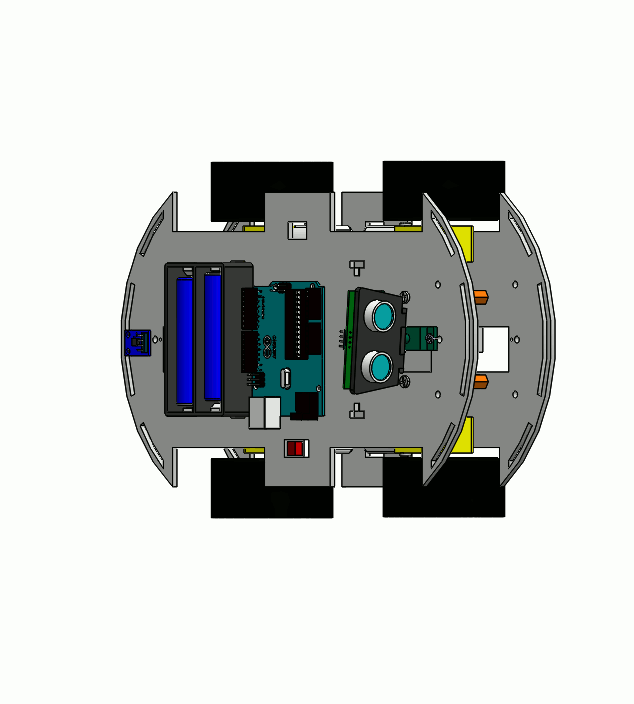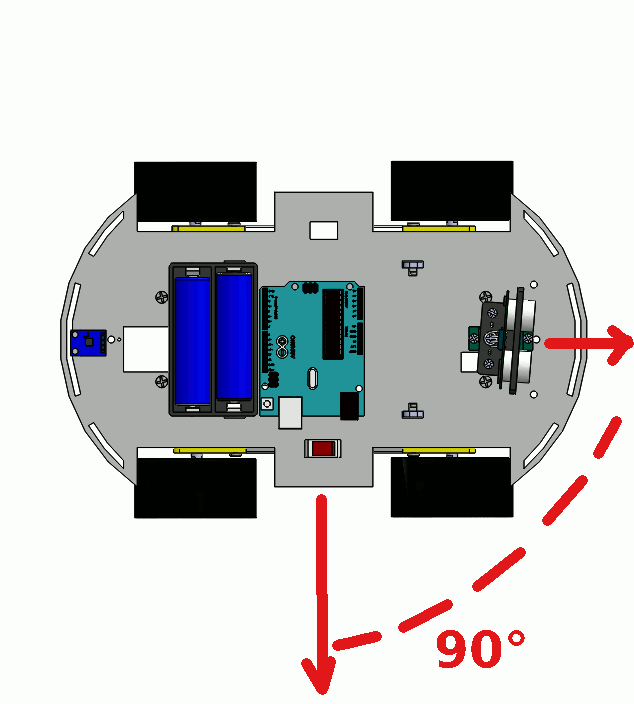
Даже поездка по относительно ровной поверхности за довольно небольшое время приведет к накоплению погрешности и смещению направления движения робота при расчете его направления с использованием только угловой скорости вокруг оси поворота.
Поэтому, для расчета углов поворота объекта относительно «мировых» координат используются более сложные расчеты. Наиболее перспективным является применение фильтра Маджвика (Madgwick). Фильтр для расчетов использует кватернионы https://ru.wikipedia.org/wiki/Кватернион
Фильтр работает быстрее, чем фильтр Кальмана (меньше расчетная нагрузка на контроллер). За основу возьмем библиотеку предложенную Олегом Евсегнеевым https://github.com/robotclass/RobotClass-MadgwickAHRS .
Для получения углов склонения робота регулярно будем производить опрос гироприбора и передавать полученные данные (угловые скорости по осям, ускорения вдоль осей) в фильтр Маджвика, а на выходе получим текущее склонение робота в кватернионах, останется перевести его в углы Эйлера (подобная функция также присутствует в библиотеке) , выбирать нужную ось и использовать угол поворота вокруг нее для анализа.
Далее приведена функция TaskCarPosition, которая является задачей под FreeRTOS (мы программируем в среде Arduino IDE, для контроллера ESP32 и используем встраиваемую ОС FreeRTOS).
Полная программа приведена в папке приложения example1.
После включения робот должен не менее 5 секунд быть неподвижен, в это время производится пересчет дрейфа нуля гироскопа, затем он начнет выдавать значения поворота в порт (скорость порта 115200). Покрутите робота убедитесь, что его угол поворота при любых вращениях остается верным.
void TaskCarPosition(void *pvParameters)
{
(void) pvParameters;
t0 = micros();
while (true)
{
// Опрос гироприбора MPU6050 (Adafruit_MPU6050)
mpu.getEvent(&a, &g, &temp);
micros_ = micros();
dt = micros_ - t0; // Длительность предыдущего периода регулирования.
t0 = micros_; //Точка начала нового периода регулирования.
double Dt = double(dt) * 0.000001;
GyroZ = g.gyro.z - CompensatorZ;
//Расчет текущего положения робота фильтром Маджвика
MadgwickAHRSupdateIMU(Dt, g.gyro.x - CompensatorX , g.gyro.y - CompensatorY, GyroZ, a.acceleration.x, a.acceleration.y, a.acceleration.z);
quat[0] = q0; quat[1] = q1; quat[2] = q2; quat[3] = q3;
// преобразуем кватернион в углы Эйлера
quat2Euler(&quat[0], &imu[0]);
if (i > 40)
{
Serial.println(imu[2] / TO_RAD);
i = 0;
}
i++;
vTaskDelay(5); //Передача управления на 5 миллисекунд (программа работает в FreeRTOS)
}
}
Задача 2. Компенсация отклонения робота от курса (заданного угла поворота)
Для решения данной задачи самое простое, что можно придумать, это пропорциональное регулирование, т.е. робот получает отклонение угла от заданного и использует его для управления моторами – пытаясь компенсировать отклонение угла. В определенных пределах это у вас получится, но точно сориентировать робота не удастся. Робот либо начнет колебаться вокруг необходимого положения, либо, если уменьшить влияние отклонения на моторы, не будет немного дотягивать до нужного положения.
Проблема решается с помощью ПИД регулятора. П-пропорциональное звено, И- интегральное звено, Д-дифференциальное звено. В нашем случае П – отклонение от заданного угла-направления, И – интеграл от отклонения по времени действия данного отклонения, Д-текущая угловая скорость (скорость с которой поворачивает робот).
Каждая составляющая ПИД регулятора настраивается, при помощи коэффициента влияния-пропорциональности, как правило данные коэффициенты подбираются экспериментально, в результате анализа поведения робота.
Angz- отклонение робота от курса, Kpz – коэффициент влияния отклонения на результат, Vz – угловая скорость или скорость поворота, Kdz – коэффициент влияния угловой скорости на результат, Iz – интеграл от Angz по времени, Kiz – коэффициент влияния Iz на результат.
Например, если повернуть робота большой угол - отклонить, и он возвращается назад рывками, значит велик коэффициент дифференциального звена. Ели робот промахивается и колеблется возле заданного значения значит скорее всего либо велико пропорциональное звено, либо мало дифференциальное. Стоит отметить, что все три звена могут приводить к колебаниям робота, но частота колебаний различна, самая высокая частота от дифференциального звена, затем идет пропорциональное звено, перебор по коэффициенту интегрального звена приведет к низкочастотным колебаниям…
Далее приведена функция регулирующая направление робота. После включения, робот принимает свое положение за «нулевое» и стремиться вернутся к нему, если его поворачивать…
void TaskCarPosition(void *pvParameters)
{
(void) pvParameters;
t0 = micros();
while (true)
{
// Опрос гироприбора MPU6050 (Adafruit_MPU6050)
mpu.getEvent(&a, &g, &temp);
micros_ = micros();
dt = micros_ - t0; // Длительность предыдущего периода регулирования.
t0 = micros_; //Точка начала нового периода регулирования.
double Dt = double(dt) * 0.000001;
GyroZ = g.gyro.z - CompensatorZ;
//Расчет текущего положения робота фильтром Маджвика
MadgwickAHRSupdateIMU(Dt, g.gyro.x - CompensatorX , g.gyro.y - CompensatorY, GyroZ, a.acceleration.x, a.acceleration.y, a.acceleration.z);
quat[0] = q0; quat[1] = q1; quat[2] = q2; quat[3] = q3;
// преобразуем кватернион в углы Эйлера
quat2Euler(&quat[0], &imu[0]);
AcZsum = imu[2]; //Вращение вокруг оси
Iz += (AcZsum - AzCom) * Dt * Kiz;
Iz = constrain(Iz, -maxIz, maxIz);
// ПИД - регулятор
PIDz = AcZsum * Kpz + GyroZ * Kdz + Iz; //Пока без интегрального звена + вправо - влево //+ dGyroZ*Kddz
PIDz = constrain( PIDz, -maxPidz, maxPidz);
// Управление моторами
MotorRight = int(-PIDz * 40.0);
MotorLeft = int(PIDz * 40.0);
// Команды моторам
RIGHTwheel_rotation(MotorRight);
LEFTwheel_rotation(MotorLeft);
vTaskDelay(5); //Передача управления на 5 миллисекунд (программа работает в FreeRTOS)
}
}
Робот начал хорошо себя вести (точно возвращаться в начальное положение) при указанных ниже значениях коэффициентов.
double Kpz = 40.0;
double Kdz = 4.00;
double Kiz = 600.0;
double maxIz = 5;
double AzCom = 0;
double maxPidz = 12;
Использовались нижеследующие настройки гироприбора:
mpu.setAccelerometerRange(MPU6050_RANGE_8_G);
mpu.setGyroRange(MPU6050_RANGE_500_DEG);
mpu.setFilterBandwidth(MPU6050_BAND_21_HZ);
Все листинги можно скачать здесь!!! В статье приведены только небольшие участки кода

ОСТАВИТЬ КОММЕНТАРИЙ
Форма авторизации
ВОЙТИ С ПОМОЩЬЮ:
ИЛИ Авторизация на сайте: